CONCEPTOS

PLANO CARTESIANO 

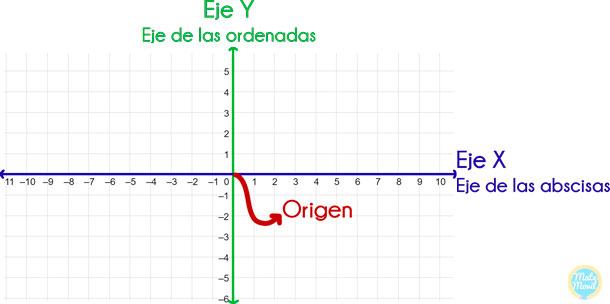
Como plano cartesiano se conoce como 2 rectas numéricas perpendiculares, una horizontal y otro vertical, que se cortan en un punto llamado origen o cero del sistema.

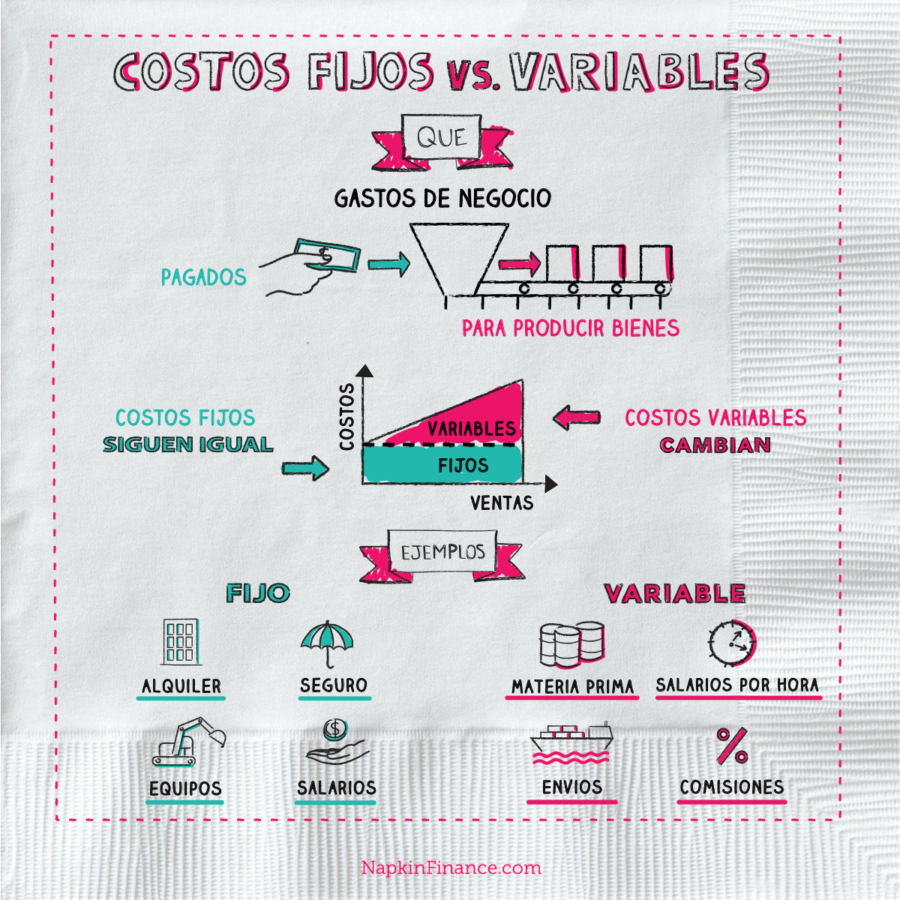
MODELO COSTO LINEAL

En la producción de cualquier bien por una empresa, intervienen dos tipos de costos; que se conocen como costos fijos y costos variables. A los costos fijos hay que enfrentarse sin importar la cantidad producida del artículo; es decir, no dependen del nivel de producción. Ejemplos de costos fijos son las rentas, intereses sobre préstamos y salarios de administración.

COSTOS FIJOS 

COSTOS VARIABLES (DEPENDE NIVEL DE PRODUCCIÓN)

DEPRECIACIÓN LINEAL

Cuando una compañía compra parte de un equipo o maquinaria, reporta el valor de

ese equipo como uno de los activos en su hoja de balance. En años subsecuentes,

este valor debe disminuir debido al lento desgaste del equipo, o bien, a que se vuelve

obsoleto. Esta reducción gradual del valor de un activo se denomina depreciación.

Un método común de calcular el monto de la depreciación es reducir el valor cada

año en una cantidad constante, de forma tal que el valor se reduzca a un valor de

desecho al final del tiempo de vida útil estimado del equipo. Esto se denomina

depreciación lineal.

EJEMPLO 3 (Depreciación) Una empresa compra maquinaria por $150,000. Se
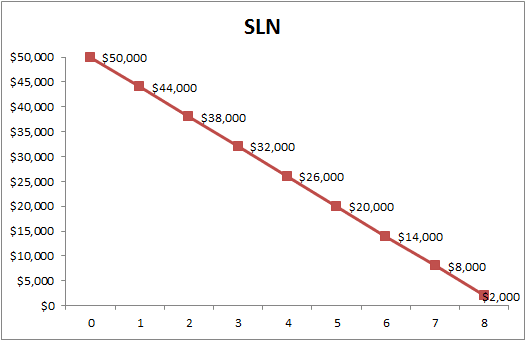
espera que el tiempo de vida útil de la maquinaria sea de 12 años con un valor de
desecho de cero. Determine el monto de depreciación anual y una fórmula para el
valor depreciado después de x años.
Solución
Depreciación por año  (Precio de adquisición inicial)

(Vida útil en años)

 (150,000 dólares)
(12 años)

 12,500 dólares

Valor después de x años  (Valor inicial)  (Depreciación por año)(Número de

años)
 (150,000 dólares)  (12,500 dólares por año)(x años)
 150,000  12,500x dólares

EJEMPLO 4 (Demanda) Un comerciante puede vender 20 rasura doras eléctricas
al día al precio de $25 cada una, pero puede vender 30 si les fija un precio de $20 a

cada rasura dora eléctrica. Determine la ecuación de demanda, suponiendo que es lineal.

Solución Considerando la cantidad x demandada como la abscisa (o coordenada x)
y el precio p por unidad como la ordenada (o coordenada y) los dos puntos sobre la
curva de demanda tienen coordenadas.

x  20, p  25 y x  30, p  20

De modo que los puntos son (20, 25) y (30, 20). Dado que la ecuación de demanda
es lineal, está dada por la ecuación de una línea recta que pasa por los puntos

(20, 25) y (30, 20). 

INFLACIÓN

Proceso económico provocado por el desequilibrio existente entre la producción y la demanda; causa una subida continuada de los precios de la mayor parte de los productos y servicios, y una pérdida del valor del dinero para poder adquirirlos o hacer uso de ellos.

ANÁLISIS PUNTO DE EQUILIBRIO 

Si el costo total yc de producción excede al de los ingresos yI obtenidos por las ventas,
entonces el negocio sufre una pérdida. Por otra parte, si los ingresos sobrepasan los
costos, existe una utilidad. Si el costo de producción es igual a los ingresos obtenidos
por las ventas, no hay utilidad ni pérdida, de modo que el negocio está en el punto de equilibrio. El número de unidades producidas y vendidas en este caso se denomina punto de equilibrio.


EJEMPLO 1 (Análisis del punto de equilibrio) Para un fabricante de relojes, el
costo de mano de obra y de los materiales por reloj es de $15 y los costos fijos son
de $2000 al día. Si vende cada reloj a $20, ¿cuántos relojes deberá producir y vender
cada día con objeto de garantizar que el negocio se mantenga en el punto de
equilibrio?
Solución Sea x el número de relojes producidos y vendidos cada día. El costo total
de producir x relojes es
yc  Costos variables totales  Costos fijos  15x  2000
Dado que cada reloj se vende a $20, el ingreso yI obtenido por vender x relojes es

yI  20x

El punto de equilibrio se obtiene cuando los ingresos son iguales a los costos, es
decir,

20x  15x  2000

Obtenemos que 5x  2000 o x  400.


De modo que deberá producir y vender al día 400 relojes para garantizar que no
haya utilidades ni pérdidas. La figura 26 da una interpretación gráfica del punto de
equilibrio. Cuando x  400, el costo yc excede a los ingresos yI y hay pérdidas.
Cuando x  400, los ingresos yI exceden los costos yc de modo que se obtiene una
utilidad.

Observe que gráficamente, el punto de equilibrio corresponde a la intersección de las dos líneas rectas. Una de las líneas tiene la ecuación y  15x  2000, la
que corresponde al costo de producción, y la otra tiene la ecuación y  20x, la que

corresponde a los ingresos.